 动态规划
动态规划
# 10.1 斐波那契数列
# 题目链接
牛客网(opens new window) (opens new window)
# 题目描述
求斐波那契数列的第 n 项,n <= 39。
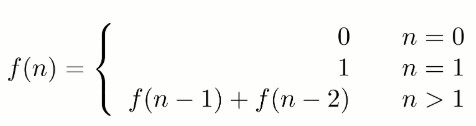
# 解题思路
如果使用递归求解,会重复计算一些子问题。例如,计算 f(4) 需要计算 f(3) 和 f(2),计算 f(3) 需要计算 f(2) 和 f(1),可以看到 f(2) 被重复计算了。
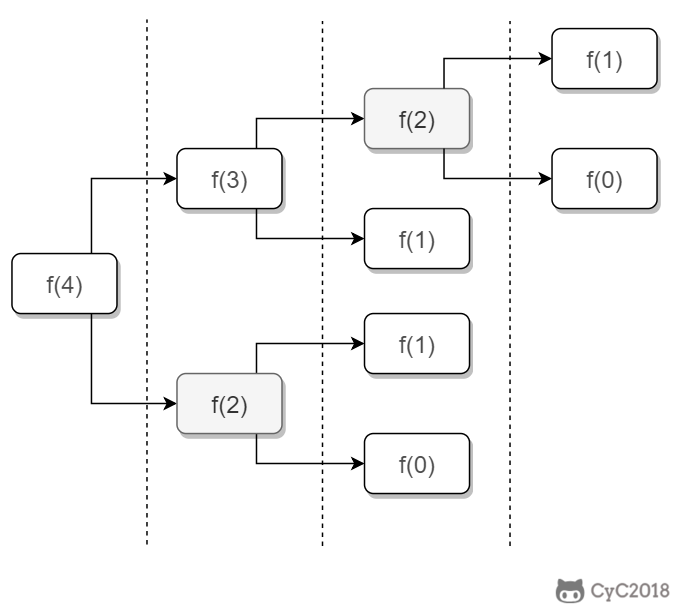
递归是将一个问题划分成多个子问题求解,动态规划也是如此,但是动态规划会把子问题的解缓存起来,从而避免重复求解子问题。
public int Fibonacci(int n) {
if (n <= 1)
return n;
int[] fib = new int[n + 1];
fib[1] = 1;
for (int i = 2; i <= n; i++)
fib[i] = fib[i - 1] + fib[i - 2];
return fib[n];
}
2
3
4
5
6
7
8
9
考虑到第 i 项只与第 i-1 和第 i-2 项有关,因此只需要存储前两项的值就能求解第 i 项,从而将空间复杂度由 O(N) 降低为 O(1)。
public int Fibonacci(int n) {
if (n <= 1)
return n;
int pre2 = 0, pre1 = 1;
int fib = 0;
for (int i = 2; i <= n; i++) {
fib = pre2 + pre1;
pre2 = pre1;
pre1 = fib;
}
return fib;
}
2
3
4
5
6
7
8
9
10
11
12
# 10.2 矩形覆盖
# 题目链接
牛客网(opens new window) (opens new window)
# 题目描述
我们可以用 21 的小矩形横着或者竖着去覆盖更大的矩形。请问用 n 个 21 的小矩形无重叠地覆盖一个 2*n 的大矩形,总共有多少种方法?

# 解题思路
当 n 为 1 时,只有一种覆盖方法:
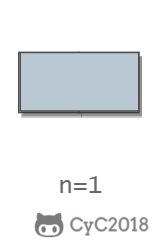
当 n 为 2 时,有两种覆盖方法:
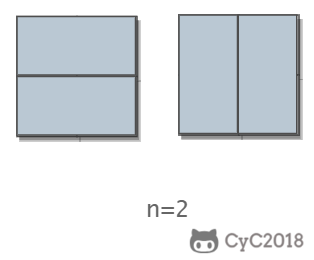
要覆盖 2n 的大矩形,可以先覆盖 21 的矩形,再覆盖 2*(n-1) 的矩形;或者先覆盖 22 的矩形,再覆盖 2(n-2) 的矩形。而覆盖 2*(n-1) 和 2*(n-2) 的矩形可以看成子问题。该问题的递推公式如下:
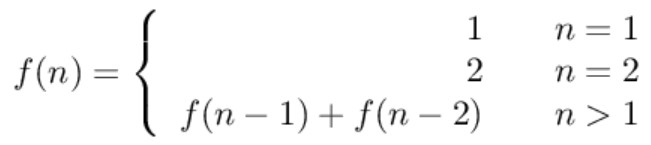
public int rectCover(int n) {
if (n <= 2)
return n;
int pre2 = 1, pre1 = 2;
int result = 0;
for (int i = 3; i <= n; i++) {
result = pre2 + pre1;
pre2 = pre1;
pre1 = result;
}
return result;
}
2
3
4
5
6
7
8
9
10
11
12
# 10.4 变态跳台阶
# 题目链接
牛客网(opens new window) (opens new window)
# 题目描述
一只青蛙一次可以跳上 1 级台阶,也可以跳上 2 级... 它也可以跳上 n 级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
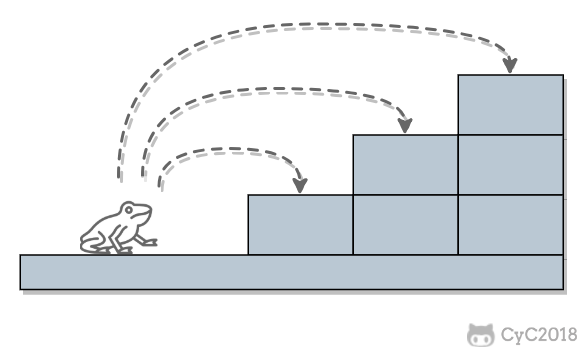
# 解题思路
# 动态规划
public int jumpFloorII(int target) {
int[] dp = new int[target];
Arrays.fill(dp, 1);
for (int i = 1; i < target; i++)
for (int j = 0; j < i; j++)
dp[i] += dp[j];
return dp[target - 1];
}
2
3
4
5
6
7
8
# 数学推导
跳上 n-1 级台阶,可以从 n-2 级跳 1 级上去,也可以从 n-3 级跳 2 级上去...,那么
f(n-1) = f(n-2) + f(n-3) + ... + f(0)
同样,跳上 n 级台阶,可以从 n-1 级跳 1 级上去,也可以从 n-2 级跳 2 级上去... ,那么
f(n) = f(n-1) + f(n-2) + ... + f(0)
综上可得
f(n) - f(n-1) = f(n-1)
即
f(n) = 2*f(n-1)
所以 f(n) 是一个等比数列
public int JumpFloorII(int target) {
return (int) Math.pow(2, target - 1);
}
2
3
# 42. 连续子数组的最大和
NowCoder(opens new window) (opens new window)
# 题目描述
{6, -3, -2, 7, -15, 1, 2, 2},连续子数组的最大和为 8(从第 0 个开始,到第 3 个为止)。
# 解题思路
public int FindGreatestSumOfSubArray(int[] array) {
int[] dp = new int[array.length];
int max = array[0];
dp[0] = array[0];
for(int i=1;i<array.length;i++){
// 动态规划,状态转移方程,确定dp[i]的最大值
dp[i] = Math.max(dp[i-1] + array[i], array[i]);
// 每次比较,保存出现的最大值
max = Math.max(max,dp[i]);
}
return max;
}
2
3
4
5
6
7
8
9
10
11
12
# 47. 礼物的最大价值
NowCoder(opens new window) (opens new window)
# 题目描述
在一个 m*n 的棋盘的每一个格都放有一个礼物,每个礼物都有一定价值(大于 0)。从左上角开始拿礼物,每次向右或向下移动一格,直到右下角结束。给定一个棋盘,求拿到礼物的最大价值。例如,对于如下棋盘
1 10 3 8
12 2 9 6
5 7 4 11
3 7 16 5
2
3
4
礼物的最大价值为 1+12+5+7+7+16+5=53。
# 解题思路
应该用动态规划求解,而不是深度优先搜索,深度优先搜索过于复杂,不是最优解。
import java.util.*;
public class Bonus {
public int getMost(int[][] board) {
if(board == null || board.length==0){
return 0;
}
for(int i=0;i<board.length;i++){
for (int j = 0; j < board[0].length; j++) {
if(i==0 && j==0){
// 奖金就是第一个格子本身
}else if(i==0){
// 说明在第一行 第一行的奖金只能来自第一行左边的格子
// 奖金等于当前格子的奖金加上左边格子的奖金
board[0][j] += board[0][j-1];
}else if(j==0){
// 说明在第一列 第一列的奖金只能来自列的上面个格子
// 奖金等于当前格子的奖金加上上面格子的奖金
board[i][0] += board[i-1][0];
}else {
// 来自上面或者左边的格子,选取最大奖金的。
// 最大奖金等于当前格子奖金加上左边或上面格子中奖金数大的那个
board[i][j] +=Math.max(board[i][j-1],board[i-1][j]);
}
}
}
// 增加通用型,直接用数据的长度吧
return board[board.length-1][board[0].length-1];
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
