数组

数组是列表的实现方式之一，也是面试中经常涉及到的数据结构。

正如前面提到的，数组是列表的实现方式，它具有列表的特征，同时也具有自己的一些特征。然而，在具体的编程语言中，数组这个数据结构的实现方式具有一定差别。比如 C++ 和 Java 中，数组中的元素类型必须保持一致，而 Python 中则可以不同。Python 中的数组叫做 list，具有更多的高级功能。

那么如何从宏观上区分列表和数组呢？这里有一个重要的概念：索引。

首先，数组会用一些名为 索引 的数字来标识每项数据在数组中的位置，且在大多数编程语言中，索引是从 0 算起的。我们可以根据数组中的索引，快速访问数组中的元素。

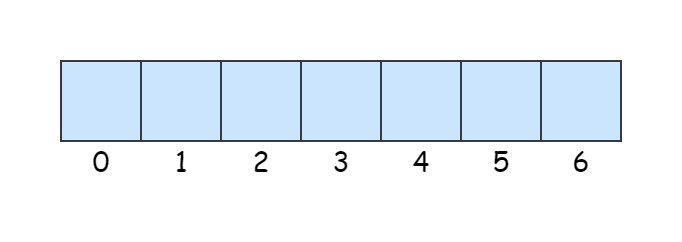
而列表中没有索引，这是数组与列表最大的不同点。

其次，数组中的元素在内存中是连续存储的，且每个元素占用相同大小的内存。

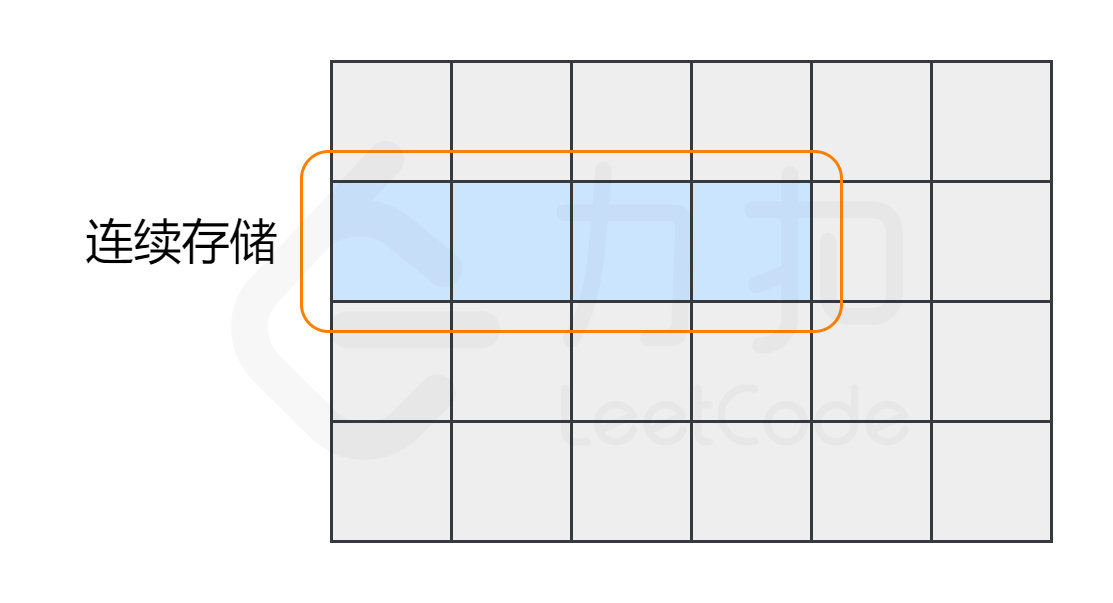
相反，列表中的元素在内存中可能彼此相邻，也可能不相邻。比如列表的另一种实现方式——链表，它的元素在内存中则不一定是连续的。

数组的操作数组的操作

读取元素

读取数组中的元素，即通过数组的索引访问数组中的元素。

这里的索引其实就是内存地址，值得一提的是，计算机可以跳跃到任意的内存地址上，这就意味着只要计算出数组中元素的内存地址，则可以一步访问到数组中的元素。

可以形象地将计算机中的内存看作一系列排列好的格子，这些格子中，每一个格子对应一个内存地址，数据会存储在不同的格子中。

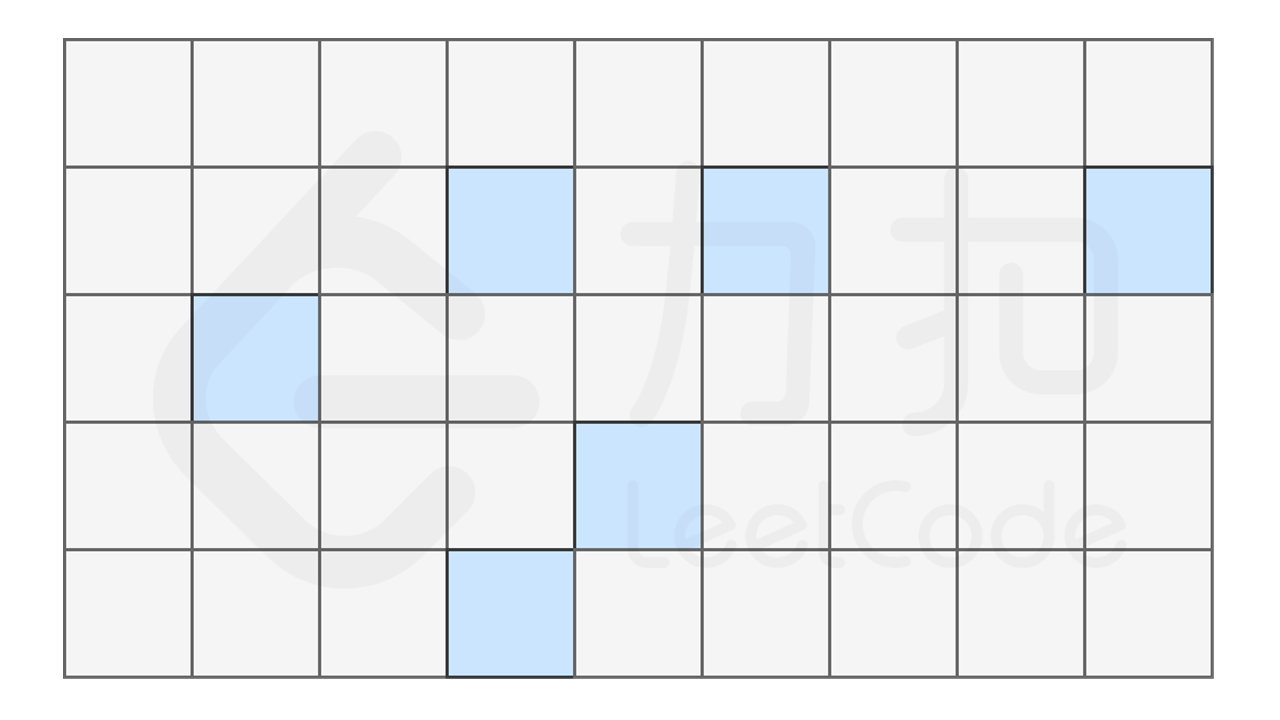
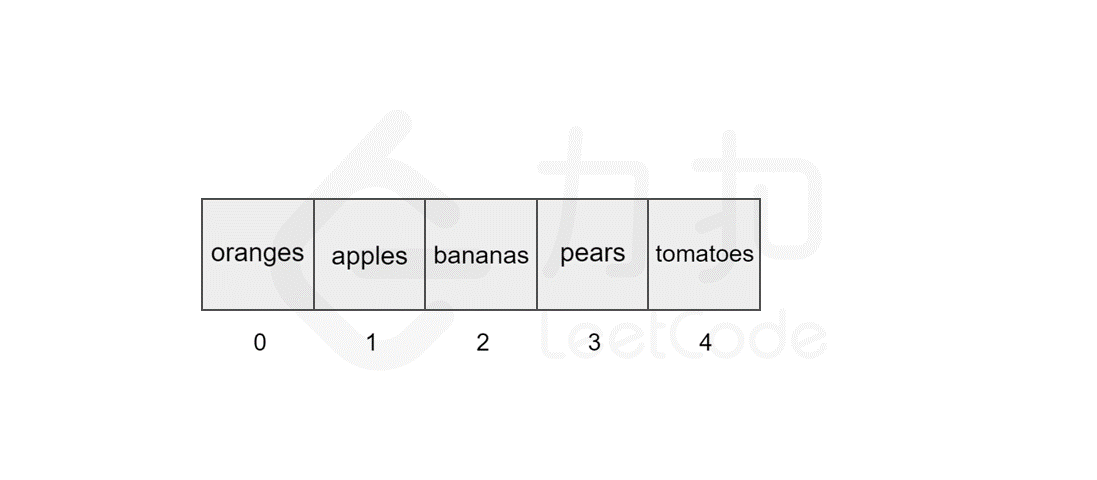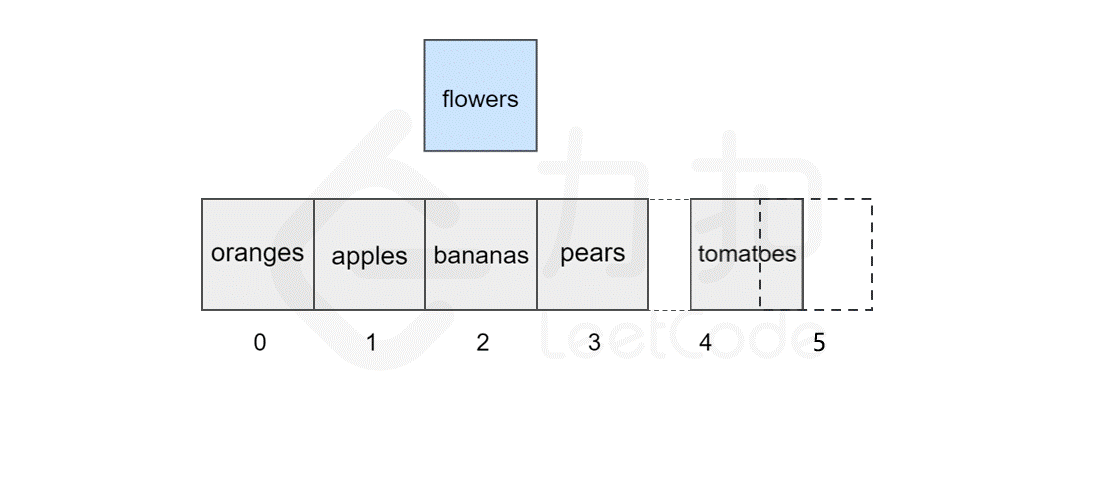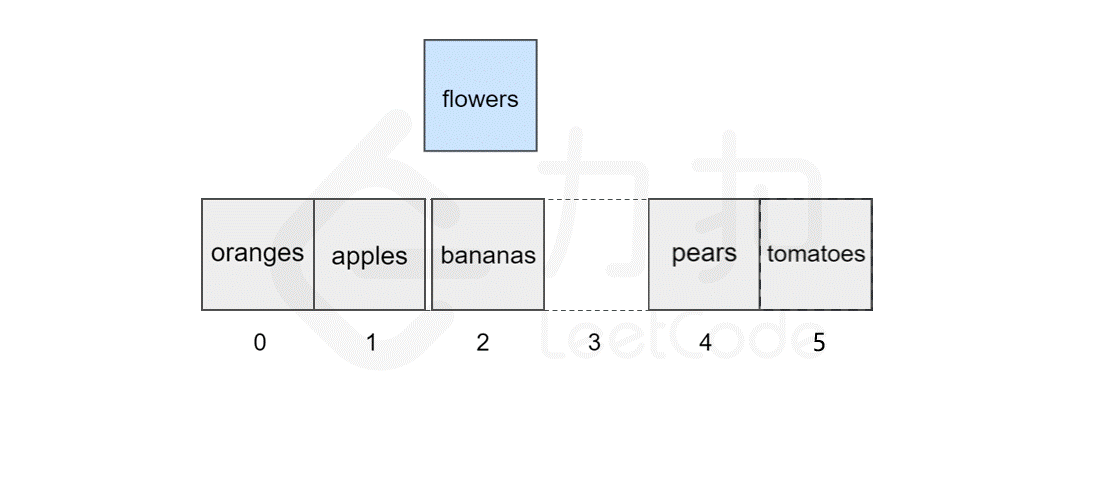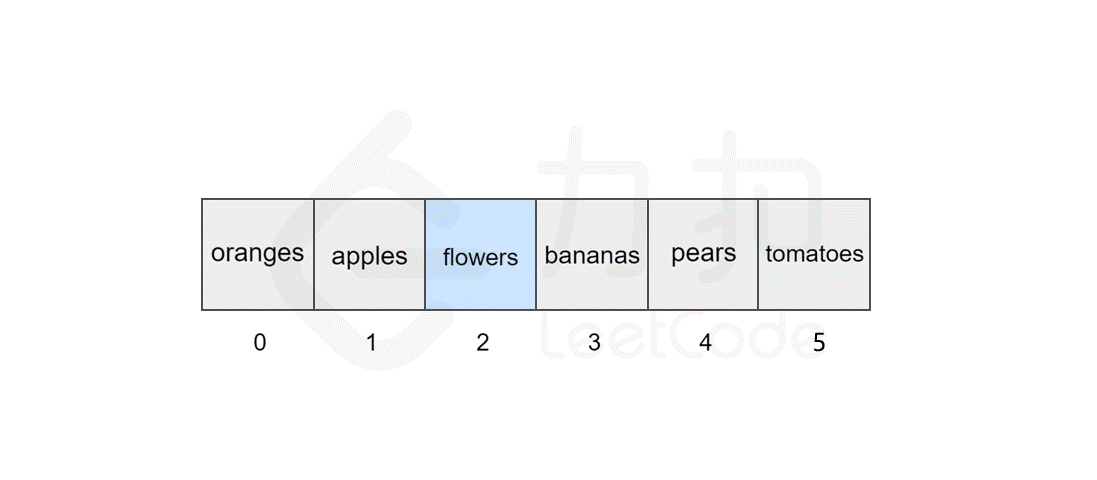
而对于数组，计算机会在内存中申请一段 连续 的空间，并且会记下索引为 0 处的内存地址。例如对于一个数组 ['oranges', 'apples', 'bananas', 'pears', 'tomatoes']，为了方便起见，我们假设每个元素只占用一个字节，它的索引与内存地址的关系如下图所示。

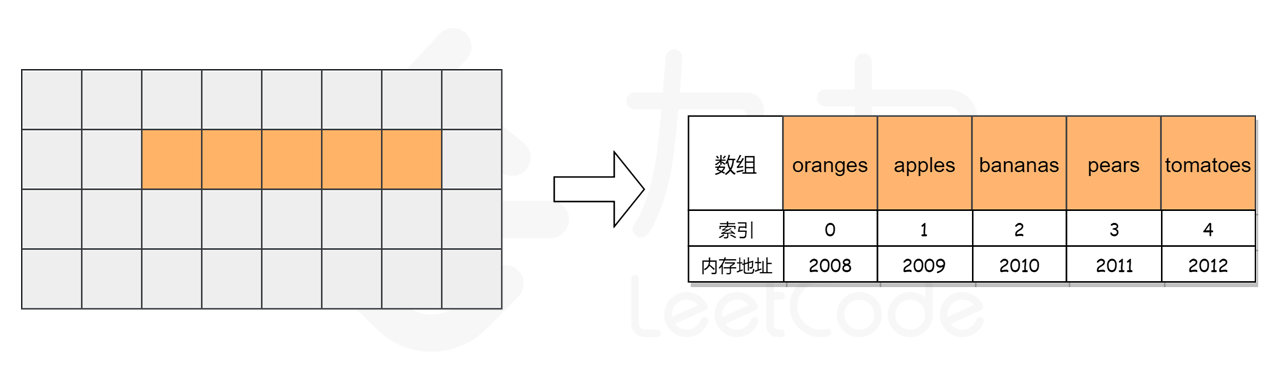
当我们访问数组中索引为 3 处的元素时，计算机会进行如下计算：

• 找到该数组的索引 0 的内存地址： 2008；
• pears 的索引为 3，计算该元素的内存地址为 2008 + 3 = 2011；

接下来，计算机就可以在直接通过该地址访问到数组中索引为 3 的元素了，计算过程很快，因此可以将整个访问过程只看作一个动作，因此时间复杂度为 。

查找元素

前面我们谈到计算机只会保存数组中索引为 0 处元素的内存地址，因此当计算机想要知道数组中是否包含某个元素时，只能从索引 0 处开始，逐步向后查询。

还是上面的例子，如果我们要查找数组中是否包含元素 pears，计算机会从索引 0 开始，逐个比较对应的元素，直到找到该元素后停止搜索，或到达数组的末尾后停止。

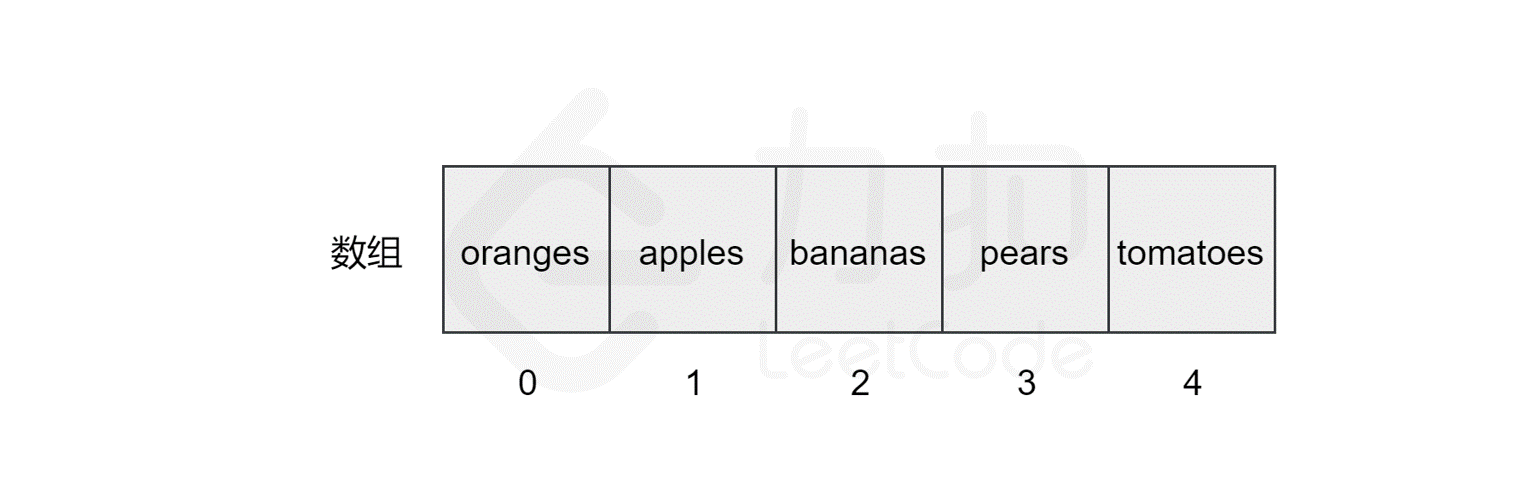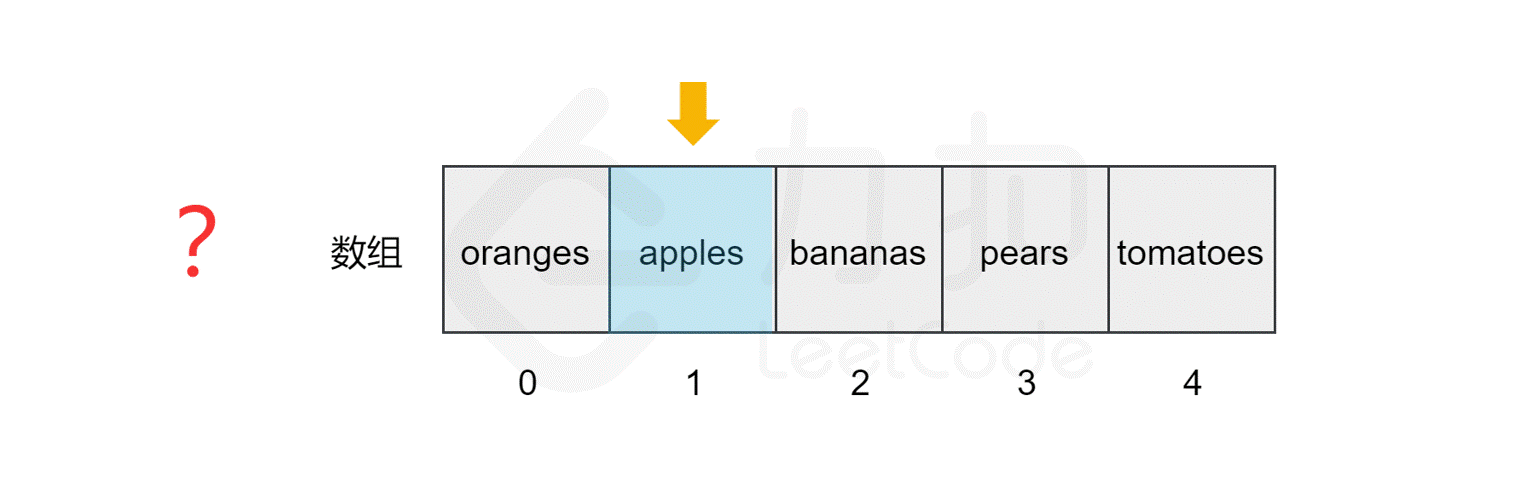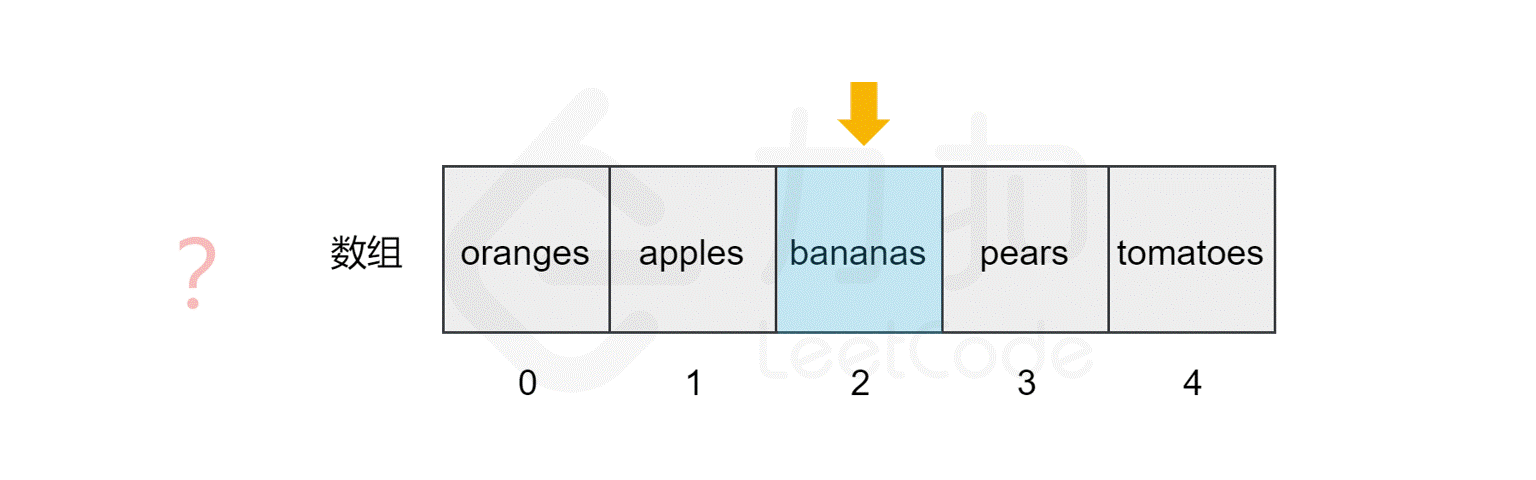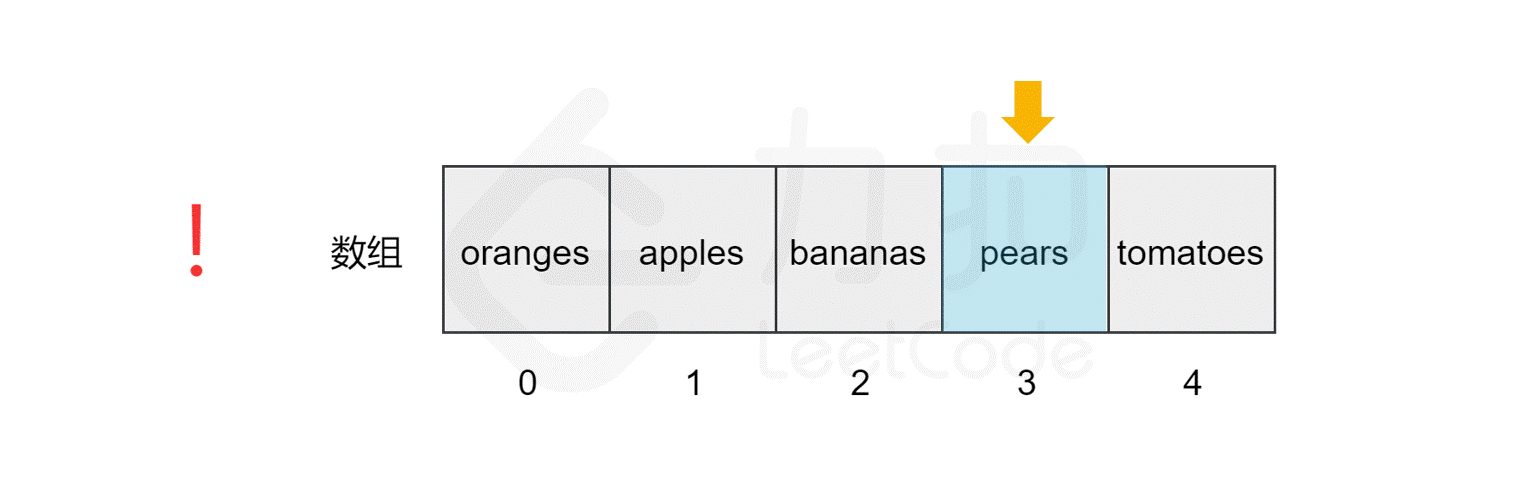
我们发现，该数组的长度为 5，最坏情况下（比如我们查找元素 tomatoes 或查找数组中不包含的元素），我们需要查询数组中的每个元素，因此时间复杂度为$ O(N)$，N 为数组的长度。

插入元素

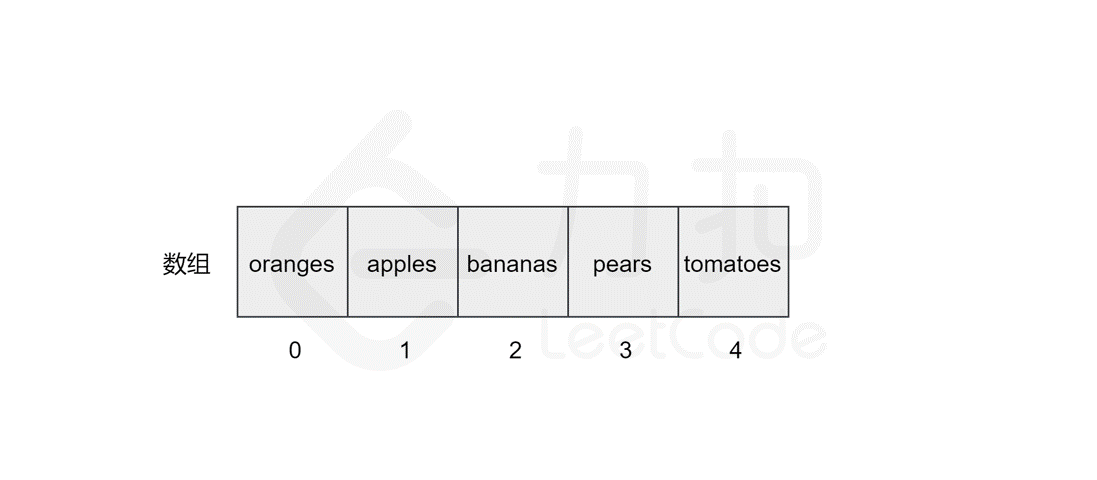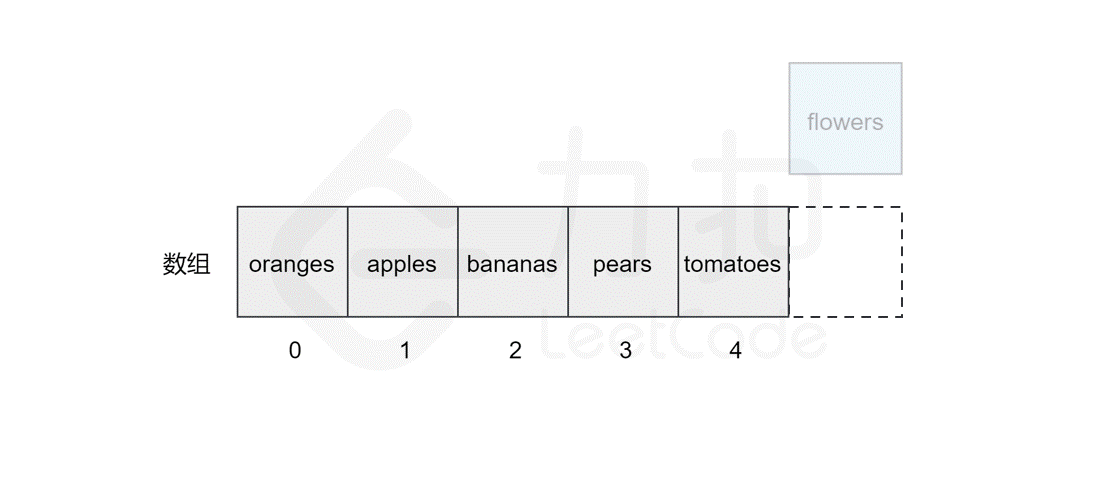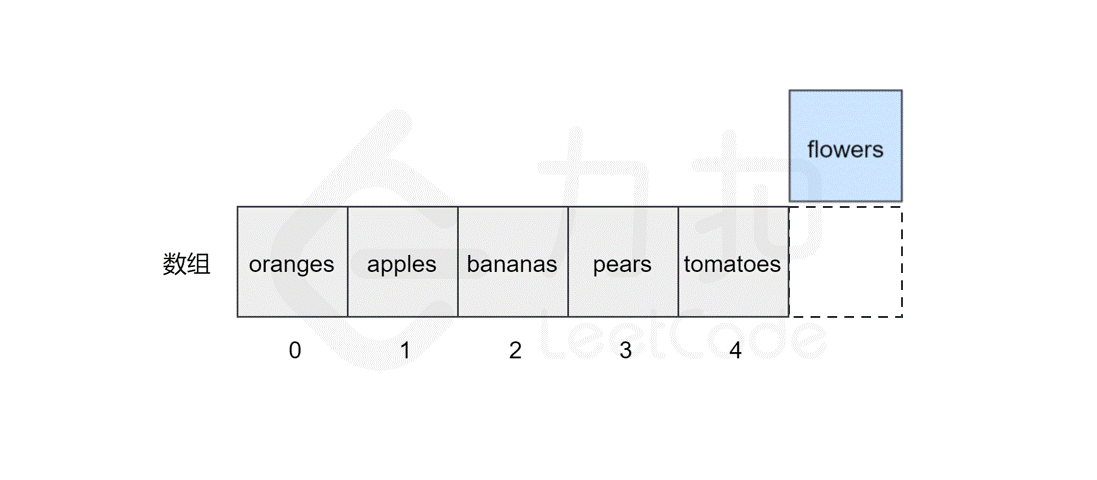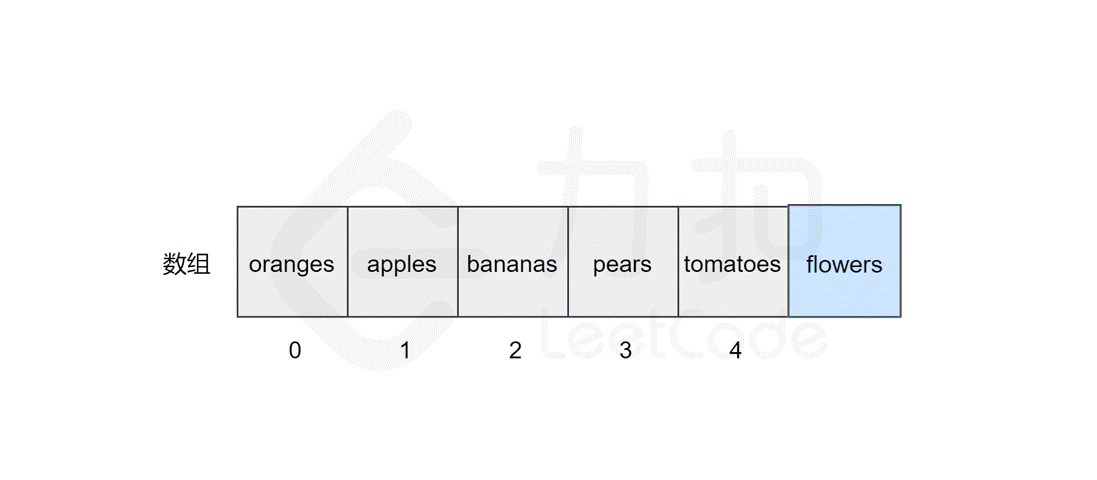
假如我们想在原有的数组中再插入一个元素 flowers 呢？

如果要将该元素插入到数组的末尾，只需要一步。即计算机通过数组的长度和位置计算出即将插入元素的内存地址，然后将该元素插入到指定位置即可。

然而，如果要将该元素插入到数组中的其他位置，则会有所区别，这时我们首先需要为该元素所要插入的位置腾出 空间，然后进行插入操作。比如，我们想要在索引 2 处插入 flowers。

我们发现，如果需要频繁地对数组元素进行插入操作，会造成时间的浪费。事实上，另一种数据结构，即链表可以有效解决这个问题。

删除元素

删除元素与插入元素的操作类似，当我们删除掉数组中的某个元素后，数组中会留下 空缺 的位置，而数组中的元素在内存中是连续的，这就使得后面的元素需对该位置进行 填补 操作。

以删除索引 1 中的元素 apples 为例，具体过程如图所示。

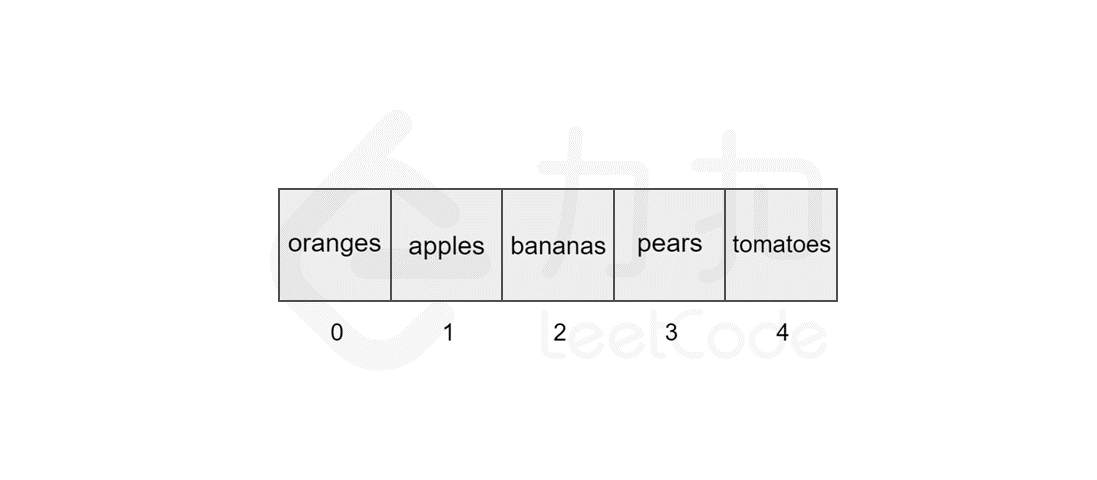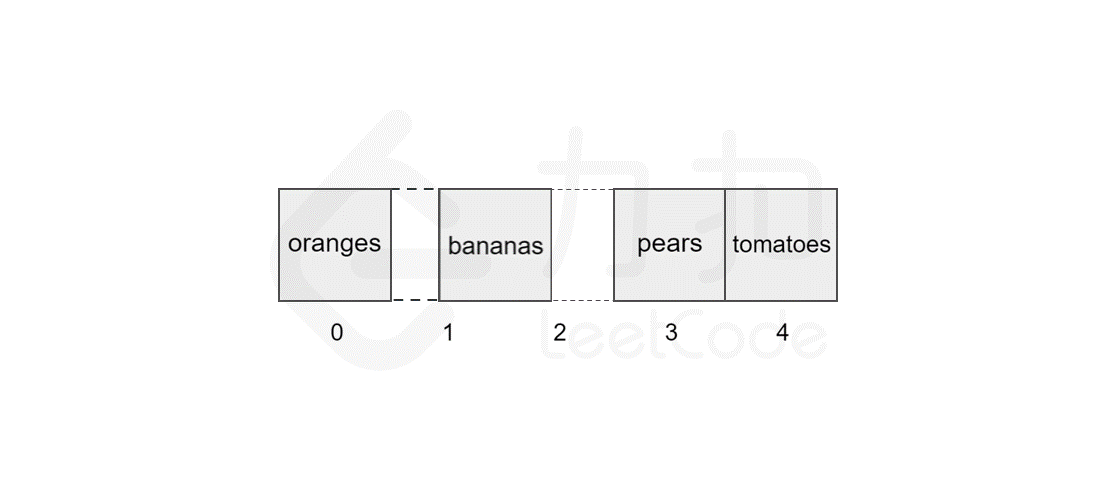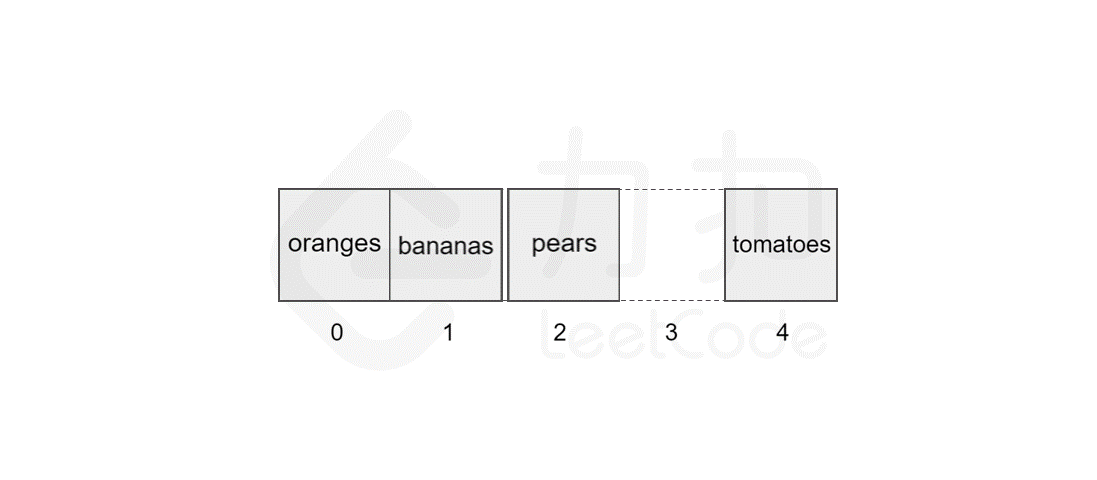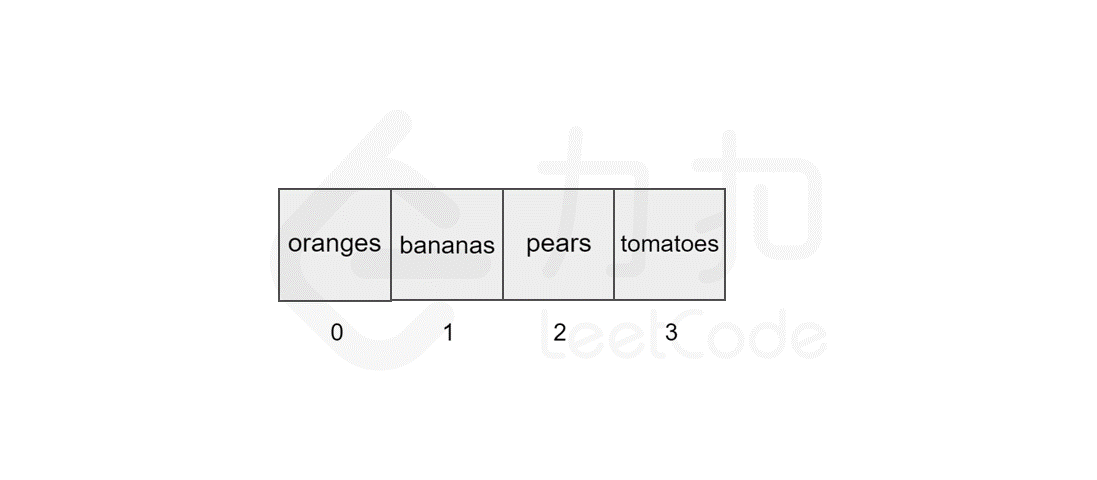
同样地，数组的长度为 5，最坏情况下，我们删除第一个元素，后面的 4 个元素需要向前移动，加上删除操作，共需执行 5 步，因此时间复杂度为 ，N 为数组的长度。

二维数组

二维数组是一种结构较为特殊的数组，只是将数组中的每个元素变成了一维数组。

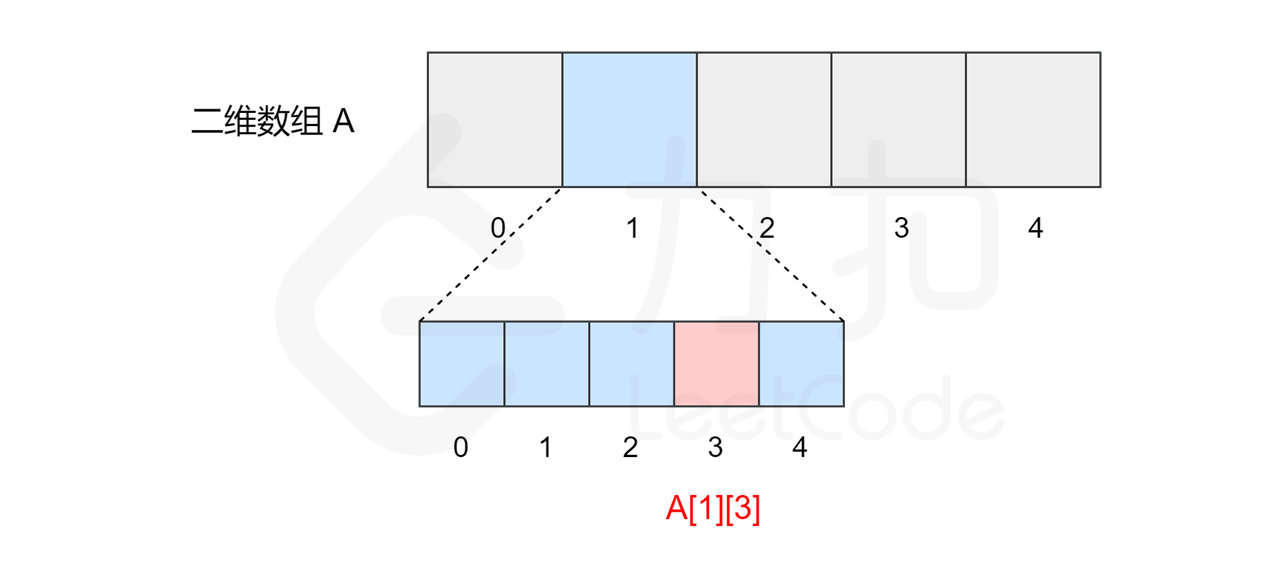
所以二维数组的本质上仍然是一个一维数组，内部的一维数组仍然从索引 0 开始，我们可以将它看作一个矩阵，并处理矩阵的相关问题。

# (opens new window)示例

类似一维数组，对于一个二维数组 A = [[1, 2, 3, 4],[2, 4, 5, 6],[1, 4, 6, 8]]，计算机同样会在内存中申请一段 连续 的空间，并记录第一行数组的索引位置，即 A[0][0] 的内存地址，它的索引与内存地址的关系如下图所示。

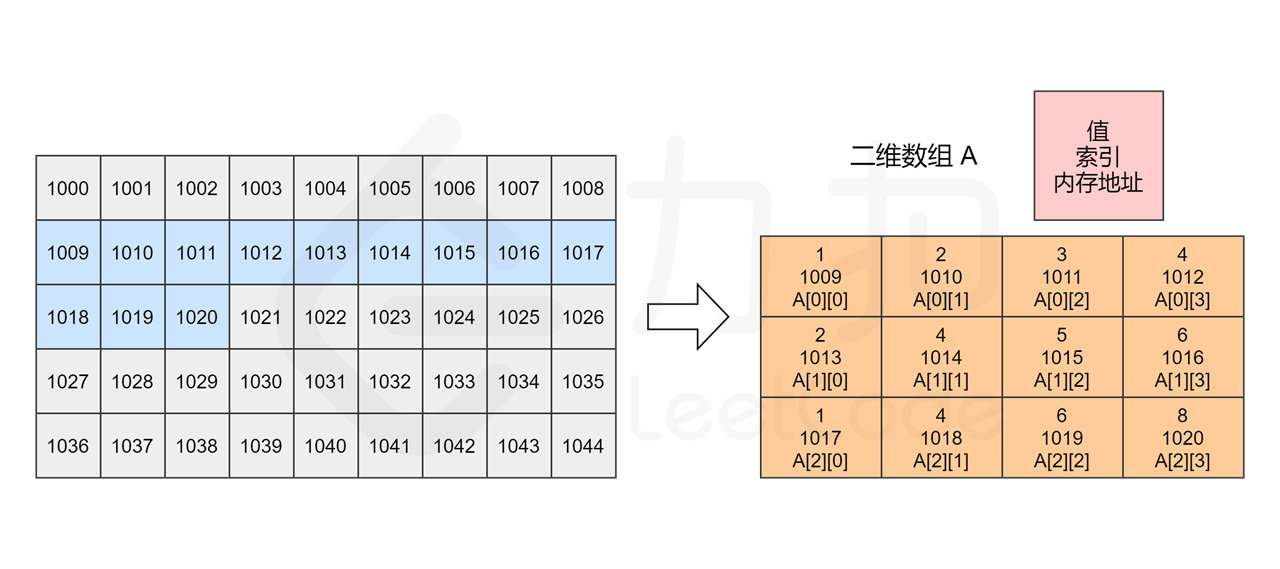
注意，实际数组中的元素由于类型的不同会占用不同的字节数，因此每个方格地址之间的差值可能不为 1。

实际题目中，往往使用二维数据处理矩阵类相关问题，包括矩阵旋转、对角线遍历，以及对子矩阵的操作等。