与数组相似，链表也是一种线性数据结构。

链表是一系列的存储数据元素的单元通过指针串接起来形成的，因此每个单元至少有两个域，一个域用于数据元素的存储，另一个域是指向其他单元的指针。这里具有一个数据域和多个指针域的存储单元通常称为结点（node）。

单链表

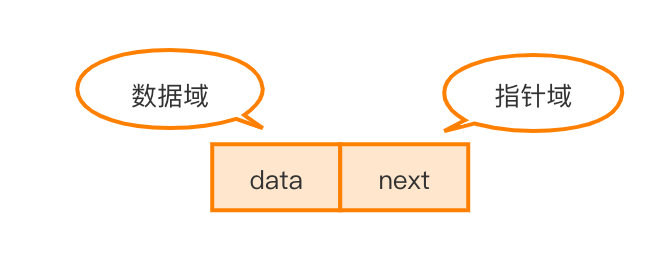
一种最简单的结点结构如上图所示，它是构成单链表的基本结点结构。在结点中数据域用来存储数据元素，指针域用于指向下一个具有相同结构的结点。

单链表中的每个结点不仅包含值，还包含链接到下一个结点的引用字段。通过这种方式，单链表将所有结点按顺序组织起来。

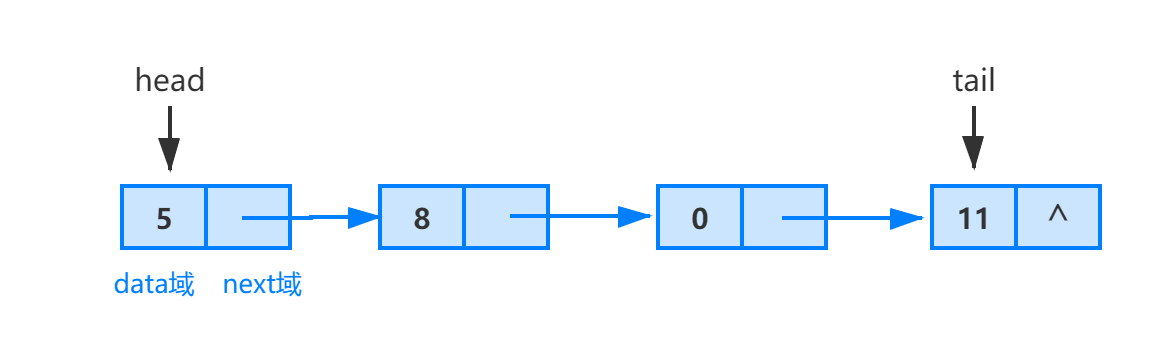
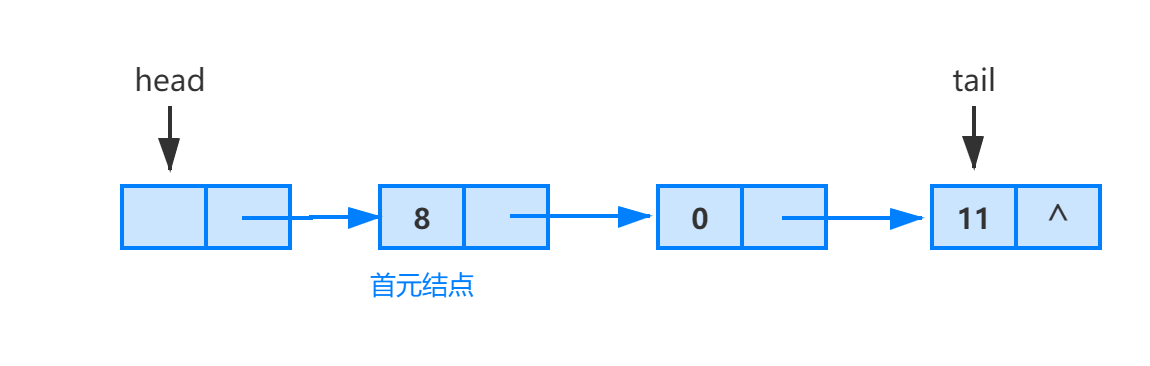
链表的第一个结点和最后一个结点，分别称为链表的首结点和尾结点。尾结点的特征是其 next 引用为空（null）。链表中每个结点的 next 引用都相当于一个指针，指向另一个结点，借助这些 next 引用，我们可以从链表的首结点移动到尾结点。如此定义的结点就称为单链表（single linked list）。

上图蓝色箭头显示单个链接列表中的结点是如何组合在一起的。

在单链表中通常使用 head 引用来指向链表的首结点，由 head 引用可以完成对整个链表中所有节点的访问。有时也可以根据需要使用指向尾结点的 tail 引用来方便某些操作的实现。

在单链表结构中还需要注意的一点是，由于每个结点的数据域都是一个 Object 类的对象，因此，每个数据元素并非真正如图中那样，而是在结点中的数据域通过一个 Object 类的对象引用来指向数据元素的。

与数组类似，单链表中的结点也具有一个线性次序，即如果结点 P 的 next 引用指向结点 S，则 P 就是 S 的直接前驱，S 是 P 的直接后续。单链表的一个重要特性就是只能通过前驱结点找到后续结点，而无法从后续结点找到前驱结点。

接着我们来看下单链表的 CRUD：

707. 设计链表 (opens new window) (opens new window)搞定一题

以下是单链表中结点的典型定义，值 + 链接到下一个元素的指针：

// Definition for singly-linked list.
public class SinglyListNode {
    int val;
    SinglyListNode next;
    SinglyListNode(int x) { val = x; }
}

有了结点，还需要一个“链” 把所有结点串起来

class MyLinkedList {
    private SinglyListNode head;
    /** Initialize your data structure here. */
    public MyLinkedList() {
        head = null;
    }
}

查找

与数组不同，我们无法在常量时间内访问单链表中的随机元素。 如果我们想要获得第 i 个元素，我们必须从头结点逐个遍历。 我们按索引来访问元素平均要花费 时间，其中 N 是链表的长度。

使用 Java 语言实现整个过程的关键语句是：

/** Get the value of the index-th node in the linked list. If the index is invalid, return -1. */
public int get(int index) {
  // if index is invalid
  if (index < 0 || index >= size) return -1;

  ListNode curr = head;
  // index steps needed 
  // to move from sentinel node to wanted index
  for(int i = 0; i < index + 1; ++i) {
    curr = curr.next;
  }
  return curr.val;
}

添加

单链表中数据元素的插入，是通过在链表中插入数据元素所属的结点来完成的。对于链表的不同位置，插入的过程会有细微的差别。

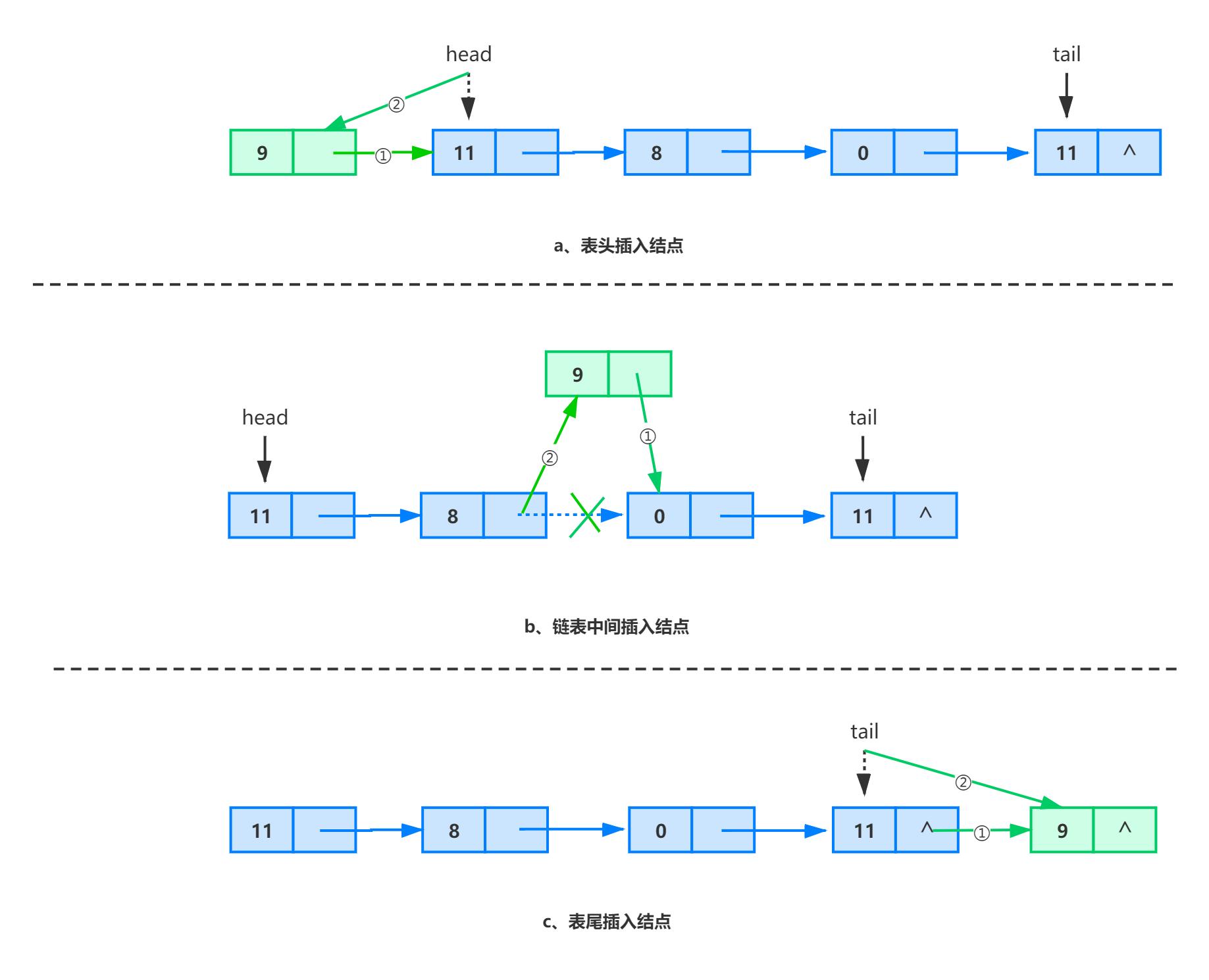
除了单链表的首结点由于没有直接前驱结点，所以可以直接在首结点之前插入一个新的结点之外，在单链表中的其他任何位置插入一个新结点时，都只能是在已知某个特定结点引用的基础上在其后面插入一个新结点。并且在已知单链表中某个结点引用的基础上，完成结点的插入操作需要的时间是 。

思考：如果是带头结点的单链表进行插入操作，是什么样子呢？

	//最外层有个链表长度，便于我们头插和尾插操作
	int size;

  public void addAtHead(int val) {
    addAtIndex(0, val);
  }

  //尾插就是从最后一个
  public void addAtTail(int val) {
    addAtIndex(size, val);
  }

  public void addAtIndex(int index, int val) {
    
    if (index > size) return;

    if (index < 0) index = 0;

    ++size;
    // find predecessor of the node to be added
    ListNode pred = head;
    for(int i = 0; i < index; ++i) {
      pred = pred.next;
    }

    // node to be added
    ListNode toAdd = new ListNode(val);
    // insertion itself
    toAdd.next = pred.next;
    pred.next = toAdd;
  }

删除

类似的，在单链表中数据元素的删除也是通过结点的删除来完成的。在链表的不同位置删除结点，其操作过程也会有一些差别。

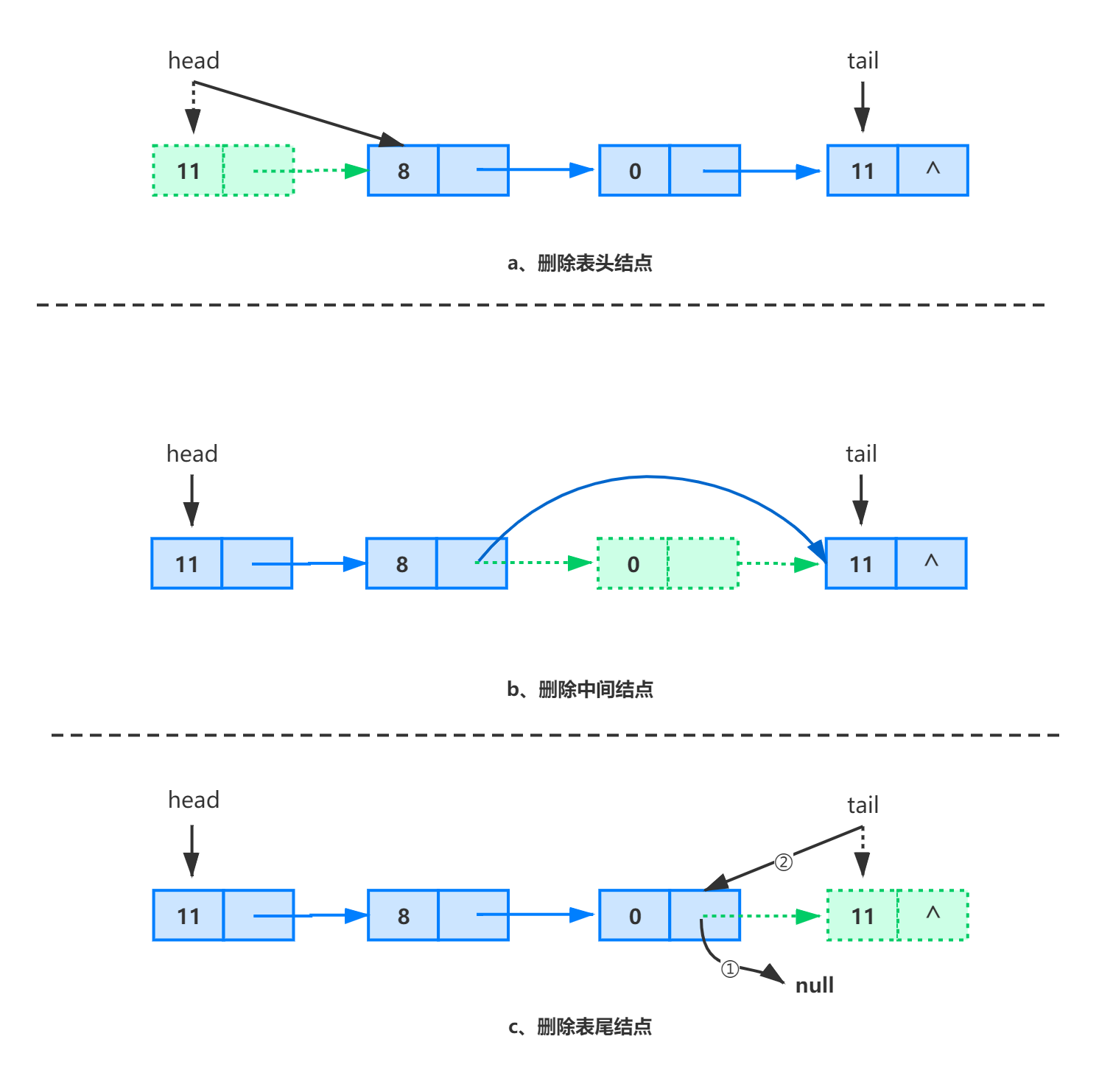
在单链表中删除一个结点时，除首结点外都必须知道该结点的直接前驱结点的引用。并且在已知单链表中某个结点引用的基础上，完成其后续结点的删除操作需要的时间是 。

在使用单链表实现线性表的时候，为了使程序更加简洁，我们通常在单链表的最前面添加一个哑元结点，也称为头结点。在头结点中不存储任何实质的数据对象，其 next 域指向线性表中 0 号元素所在的结点，头结点的引入可以使线性表运算中的一些边界条件更容易处理。

对于任何基于序号的插入、删除，以及任何基于数据元素所在结点的前面或后面的插入、删除，在带头结点的单链表中均可转化为在某个特定结点之后完成结点的插入、删除，而不用考虑插入、删除是在链表的首部、中间、还是尾部等不同情况。

  public void deleteAtIndex(int index) {
    // if the index is invalid, do nothing
    if (index < 0 || index >= size) return;

    size--;
    // find predecessor of the node to be deleted
    ListNode pred = head;
    for(int i = 0; i < index; ++i) {
      pred = pred.next;
    }

    // delete pred.next 
    pred.next = pred.next.next;
  }

双向链表

单链表的一个优点是结构简单，但是它也有一个缺点，即在单链表中只能通过一个结点的引用访问其后续结点，而无法直接访问其前驱结点，要在单链表中找到某个结点的前驱结点，必须从链表的首结点出发依次向后寻找，但是需要 时间。

所以我们在单链表结点结构中新增加一个域，该域用于指向结点的直接前驱结点。

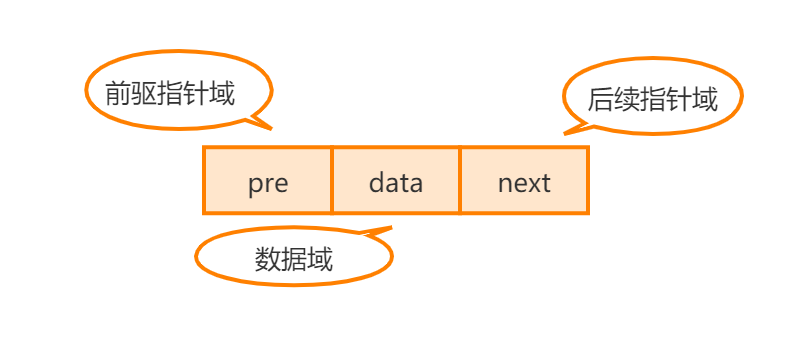
双向链表是通过上述定义的结点使用 pre 以及 next 域依次串联在一起而形成的。一个双向链表的结构如下图所示。

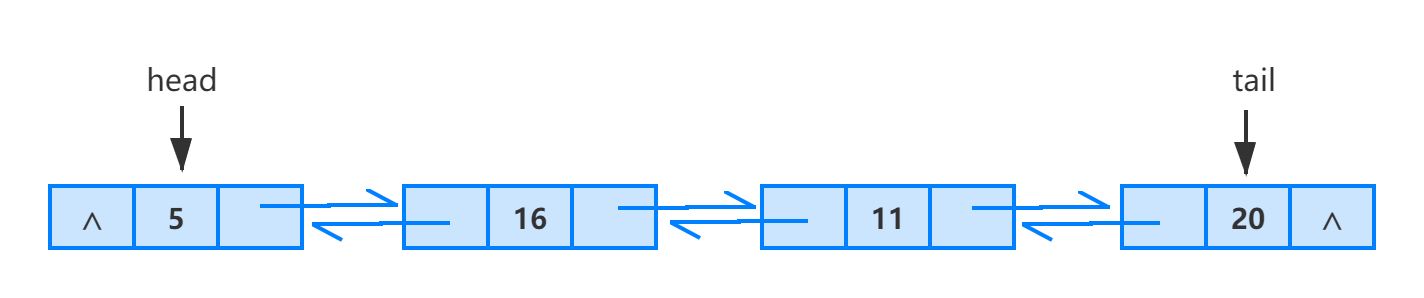
接着我们来看下双向链表的 CRUD：

以下是双链表中结点的典型定义：

public class ListNode {
  int val;
  ListNode next;
  ListNode prev;
  ListNode(int x) { val = x; }
}

class MyLinkedList {
  int size;
  // sentinel nodes as pseudo-head and pseudo-tail
  ListNode head, tail;
  public MyLinkedList() {
    size = 0;
    head = new ListNode(0);
    tail = new ListNode(0);
    head.next = tail;
    tail.prev = head;
  }

查找

在双向链表中进行查找与在单链表中类似，只不过在双向链表中查找操作可以从链表的首结点开始，也可以从尾结点开始，但是需要的时间和在单链表中一样。

  /** Get the value of the index-th node in the linked list. If the index is invalid, return -1. */
  public int get(int index) {
    if (index < 0 || index >= size) return -1;

    ListNode curr = head;
    if (index + 1 < size - index)
      for(int i = 0; i < index + 1; ++i) {
        curr = curr.next;
      }
    else {
      curr = tail;
      for(int i = 0; i < size - index; ++i) {
        curr = curr.prev;
      }
    }

    return curr.val;
  }

添加

单链表的插入操作，除了首结点之外必须在某个已知结点后面进行，而在双向链表中插入操作在一个已知的结点之前或之后都可以进行，如下表示在结点 11 之前 插入 9。

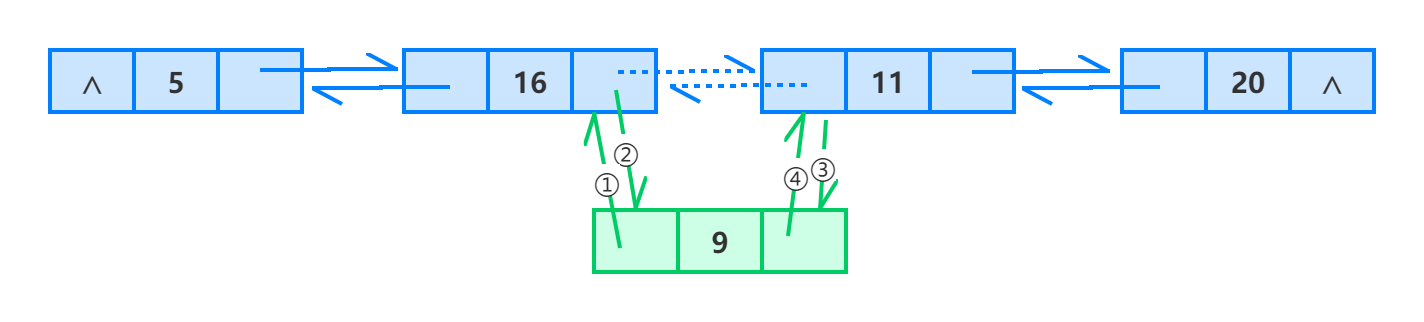
使用 Java 语言实现整个过程的关键语句是

  public void addAtHead(int val) {
    ListNode pred = head, succ = head.next;

    ++size;
    ListNode toAdd = new ListNode(val);
    toAdd.prev = pred;
    toAdd.next = succ;
    pred.next = toAdd;
    succ.prev = toAdd;
  }

  /** Append a node of value val to the last element of the linked list. */
  public void addAtTail(int val) {
    ListNode succ = tail, pred = tail.prev;

    ++size;
    ListNode toAdd = new ListNode(val);
    toAdd.prev = pred;
    toAdd.next = succ;
    pred.next = toAdd;
    succ.prev = toAdd;
  }

  public void addAtIndex(int index, int val) {
    if (index > size) return;

    if (index < 0) index = 0;

    ListNode pred, succ;
    if (index < size - index) {
      pred = head;
      for(int i = 0; i < index; ++i) pred = pred.next;
      succ = pred.next;
    }
    else {
      succ = tail;
      for (int i = 0; i < size - index; ++i) succ = succ.prev;
      pred = succ.prev;
    }

    // insertion itself
    ++size;
    ListNode toAdd = new ListNode(val);
    toAdd.prev = pred;
    toAdd.next = succ;
    pred.next = toAdd;
    succ.prev = toAdd;
  }

在结点 p 之后插入一个新结点的操作与上述操作对称，这里不再赘述。

插入操作除了上述情况，还可以在双向链表的首结点之前、双向链表的尾结点之后进行，此时插入操作与上述插入操作相比更为简单。

删除

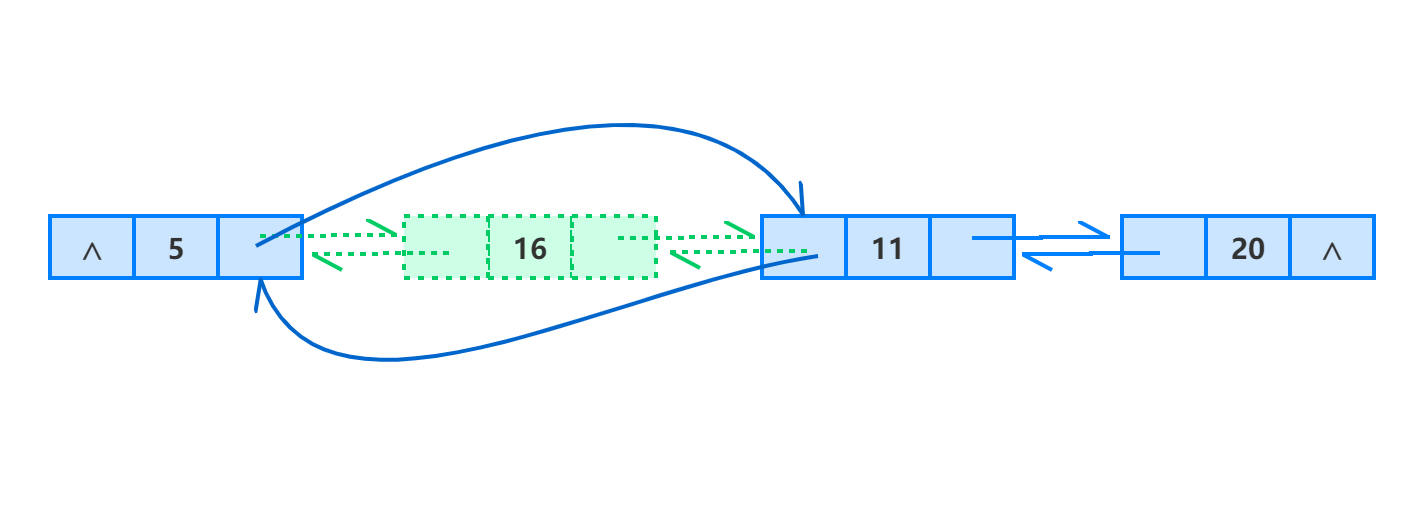
单链表的删除操作，除了首结点之外必须在知道待删结点的前驱结点的基础上才能进行，而在双向链表中在已知某个结点引用的前提下，可以完成该结点自身的删除。如下表示删除 16 的过程。

	/** Delete the index-th node in the linked list, if the index is valid. */
  public void deleteAtIndex(int index) {
    if (index < 0 || index >= size) return;

    ListNode pred, succ;
    if (index < size - index) {
      pred = head;
      for(int i = 0; i < index; ++i) pred = pred.next;
      succ = pred.next.next;
    }
    else {
      succ = tail;
      for (int i = 0; i < size - index - 1; ++i) succ = succ.prev;
      pred = succ.prev.prev;
    }

    // delete pred.next 
    --size;
    pred.next = succ;
    succ.prev = pred;
  }
}

对线性表的操作，无非就是排序、加法、减法、反转，说的好像很简单，我们去下一章刷题吧

参考

链表 (opens new window)